Getting connected - The highly connected society
Densely connected networks
A dense network is a network in which the number of links of each node is close to the maximal number of nodes. Each node is linked to almost all other nodes. The total connected case in which exactly each node is linked to each other node is called a completely connected network. Examples of higher link density are epidemic spreading, the neural network of the brain and telecommunication networks.A sparse network, by contrast, is connected by a low number of links only. A sparse connectivity can be found in networks in which links are more difficult to create. This includes citation networks, friendship-networks, and power-line network.
To measure the link density (edge density) of a network, we calculate the ratio of existing links m to the total number of possible links. For a network of N nodes, the network link density is D = m / 0.5*N*(N-1)
The (maximal) link density D of a completely connected network is 1.
Epidemic spreading
Many infectious diseases such as common cold and influenza can be easily spread when an infected person sneezes or coughs next to another person. To get a realistic model for predicting epidemic spreading, we have to consider all possible contacts including very weak links between people, e.g., sitting next to each other in a train. This means we have to consider networks of much higher link density than normally found in contact or friendship networks.Neuroscience
The neurons of the brain are often organized as a densely connected network. This suggest that a dense network structure might be advantageous for information processing. Results from research of dense networks can give us new ideas about how our brain works.Languages
How does increasing world-wide communication affect our language? Is English on the way to displace other languages? It might come true what is aptly described by the Italian writer Luciano De Crescenzo in Il caffè sospeso (2008):“...diminuiscono le differenze tra gli esseri umani: spariscono i dialetti a favore dell'italiano, spariscono le lingue (e con esse l'italiano) a favore dell'inglese.”
“...the differences between human beings decrease: dialects disappear in favor of Italian, languages disappear (and with them Italian) in favor of English.”
It is more the personal increase in the number of diverse contacts across the world (increasing link degree and density) than an increase in total communication intensity that drives such development.
Society
If people become more and more connected, how does this affect our society? First results show that individuals of a highly connected society are more equally linked to each other. This in turn gives more equal influence and power to all members of a society. There is no “unfair” hierarchic scale-free power-law anymore. Consequently, the transition from weakly to strongly connected societies will have strong impacts - socially, economically, and politically.From lowly connected to highly connected networks
A data analysis of the Flickr social online network (Scholz 2015).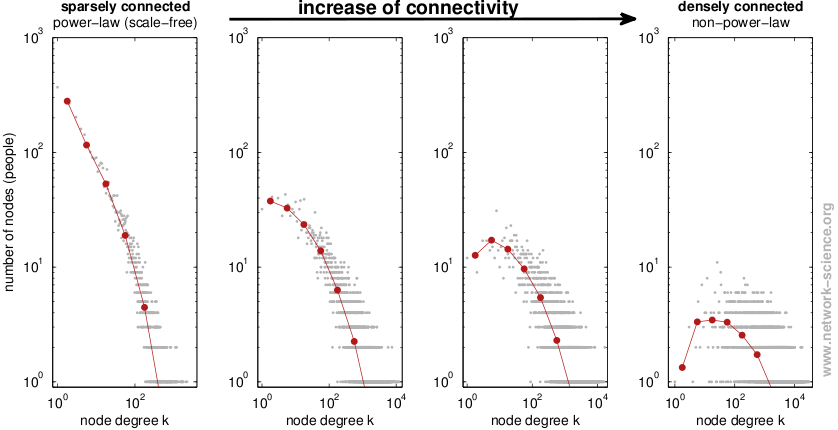
To retrieve a realistic dense network we count all links, including weak links of interactions. As a result, this study shows that the network link structure changes with increasing connectivity. Sparsely connected networks (left) show the typical power-law (scale-free) node-degree distribution in which most nodes have only few links while some few nodes are extremely linked. By contrast, densely connected networks (right), show a more “fair” distribution of less differences between lowly and highly linked nodes.
A model for dense networks. To reproduce the characteristics of the transitions from sparse to dense networks, a simple network formation model based on node similarity can be used.